The Geometer's Sketchpad
Modeling a Ferris Wheel
Using Translations and Animation

Original version by Jim King.
Adapted by Pat Brewster, for updated Version 4.05 of Geometer's Sketchpad

   Modeling a Ferris Wheel

Physical devices can be modeled using dynamic geometry. A vital tool for moving objects around in the model are the isometries, or distance-preserving transformations. This model of a Ferris wheel provides a good example.

Begin with a circle and a template for the chair.
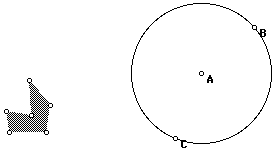
  • Start a new sketch and draw a circle; then add point C as a Point on Object that slides around the circle. 
  • Also, create a chair-shaped blob as a Polygon Interior.
An animation button for C. 
 
  • We wish to animate C so that it runs around its circle. Select the point C, only.
  • Now we choose an item on a submenu. Press the mouse button down on the Action Button Item of the Edit menu and then slide the mouse to the right and down to choose Animation....
  • You will get a dialog box with some choices. This time just click Okay for the tab  that says Animate.
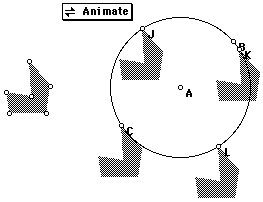
  • An animation button appears in the sketch. Click on the button to send the point C running around the circle. 
  • To stop the animation, click again on the Animate Button. 
  • Add a segment. Construct the radial segment AC . Use the Select Arrow, on the toolbar at the left. Click the Animate Button again. What happens to the segment?
Attach a chair at point C using a translation.
 
  • We will mark a vector from a vertex of the blob to point C. Select one of the vertices of the blob and then point C. Now choose Mark Vector .
  • Select the blob by dragging a rectangle around it.  Translate the blob by the marked vector. Use the Transform Pull-down menue. (Choose Translate, by Marked Vector.) Where does the blob move?  (QUESTION #1a) What happens when you drag point C. (QUESTION #1b)  Why? (QUESTION #1c)
  • Now Click the Animate button again. What happens? (QUESTION #2a)Why? (QUESTION #2b) In the figure, can you tell which vertex on the blob was selected when marking the vector? (QUESTION #2c)
Adding more seats.
This Ferris wheel has just one seat. Let's add more seats. We will do this by constructing 3 more points on the circle to which we will attach the seats. These points, along with C, will make four points, equally spaced 90 degrees apart around the circle.
  • Construct these points by constructing the line AC and then the line through A perpendicular to line AC. The points of intersection of these lines with the circle are the four equally spaced points.
  • Run the animation again to see how the four points move in unison. Hide the two lines, and segment AC,  for esthetic reasons. (Select the lines, and segment, then click on Display, the Hide Lines.)
  • Now in turn mark the vector from the same vertex of the blob as before to each of these three new points. Each time you mark a vector, translate the blob by this vector. (Unselect the blob, before setting up the next translation of a chair.)
  • Now double-click the animate button again to see your Ferris wheel.
  • Select the vertices of your blob, then Construct Polygon Interior.  Use Display, to change the colors of your "seats."

To Save your sketch in the computer lab, save it in the Brewster Folder, in the Period folder for your class.
Save it as: Your last name, first name, Ferris Wheel #1


Refinements and Extensions. 
Ferris Wheel #2
Adjustable seats. Since this construction is dynamic, we can make changes. Drag some vertices of the original blob to reshape the "seat." Can you make the seats face the opposite way as before?
Save it as: Your last name, first name, Ferris Wheel #2

Ferris Wheel #3
A six-seater. Make another Ferris wheel with six seats.
Hint: Use the Transform pull-down menu to get the seats equally spaced.  Use Mark Center, and use Rotate. 
Save it as: Your last name, first name, Ferris Wheel #3

Wrap-up
Write a Reflection paragraph about this extra credit project.  Include:

  • Was this easy or difficult for you?
  • Did you get help?
  • Would you like to do another Extra Credit Geometer's Sketchpad project?
E  N  D

Click here»       to return to Home Page.